
P, Q, R, and S are the vertices of a closed figure.If the figure is 90 from the origin in a clockwise direction, you can find the vertices of it.Īfter rotating 90 degrees clockwise about the origin, can you find the new position of the given coordinates?Īfter applying this rule, it changes into new coordinates. The new place of the above coordinates can be found when the point rotates through 90o. Our point becomes M'(y,-x) if a point is rotating 90 degrees clockwise.If you want to make x negative, switch x and y.ĭo you know the coordinates of the points that are rotating through a 90 clockwise direction? In this article, we are going to discuss the 90 Degree Clockwise Rotation like definition, rule, how it works, and some solved examples.This is an article, let's get into it!
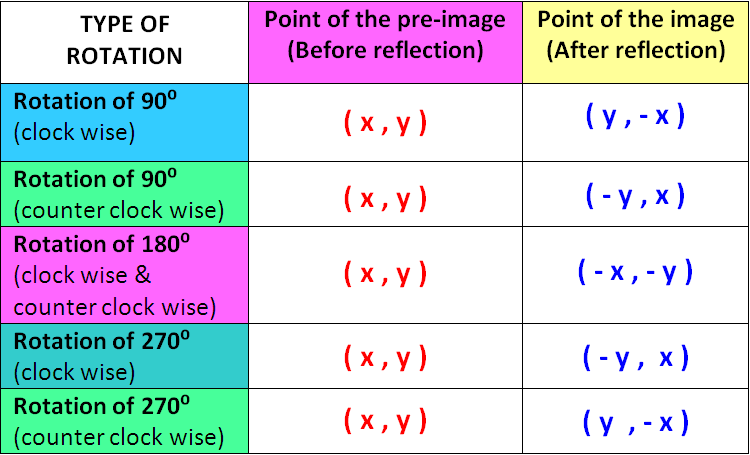
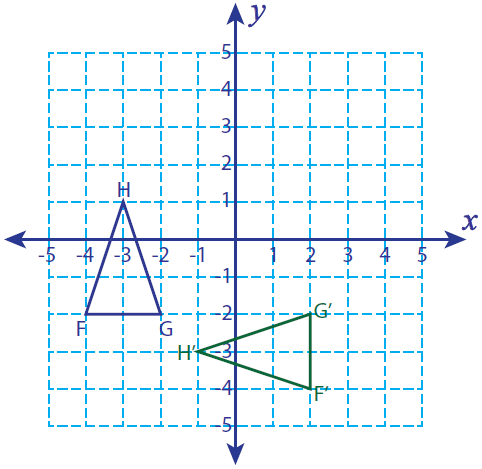
Rotations is the most common topic in Geometry Topics.A rotation is a circular motion of a figure or object.The Earth rotates on its own axis if we talk about real-life examples.The rotation can work in both directions.The most common rotation angles are 90 and 180. Then the 180 degrees look like a Straight Line.90 degree clockwise rotation rule, what is it? The measure of 180 degrees in an angle is known as Straight angles. Yes, both are different but the formula or rule for 180-degree rotation about the origin in both directions clockwise and anticlockwise is the same. Is turning 180 degrees clockwise different from turning 180 degrees counterclockwise? The rule for a rotation by 180° about the origin is (x,y)→(−x,−y).Ģ. FAQs on 180 Degree Clockwise & Anticlockwise Rotation Given coordinate is A = (2,3) after rotating the point towards 180 degrees about the origin then the new position of the point is A’ = (-2, -3) as shown in the above graph. Put the point A (2, 3) on the graph paper and rotate it through 180° about the origin O. (iv) The new position of the point S (1, -3) will be S’ (-1, 3) (iii) The new position of the point R (-2, -6) will be R’ (2, 6) (ii) The new position of the point Q (-5, 8) will be Q’ (5, -8) (i) The new position of the point P (6, 9) will be P’ (-6, -9) By applying this rule, here you get the new position of the above points: The rule of 180-degree rotation is ‘when the point M (h, k) is rotating through 180°, about the origin in a Counterclockwise or clockwise direction, then it takes the new position of the point M’ (-h, -k)’. Worked-Out Problems on 180-Degree Rotation About the Originĭetermine the vertices taken on rotating the points given below through 180° about the origin. If the point (x,y) is rotating about the origin in 180-degrees counterclockwise direction, then the new position of the point becomes (-x,-y).If the point (x,y) is rotating about the origin in 180-degrees clockwise direction, then the new position of the point becomes (-x,-y).So, the 180-degree rotation about the origin in both directions is the same and we make both h and k negative.
When the point M (h, k) is rotating through 180°, about the origin in a Counterclockwise or clockwise direction, then it takes the new position of the point M’ (-h, -k). Check out this article and completely gain knowledge about 180-degree rotation about the originwith solved examples. Both 90° and 180° are the common rotation angles. One of the rotation angles ie., 270° rotates occasionally around the axis. Generally, there are three rotation angles around the origin, 90 degrees, 180 degrees, and 270 degrees. Any object can be rotated in both directions ie., Clockwise and Anticlockwise directions. Rotation in Maths is turning an object in a circular motion on any origin or axis. Students who feel difficult to solve the rotation problems can refer to this page and learn the techniques so easily.


 0 kommentar(er)
0 kommentar(er)
